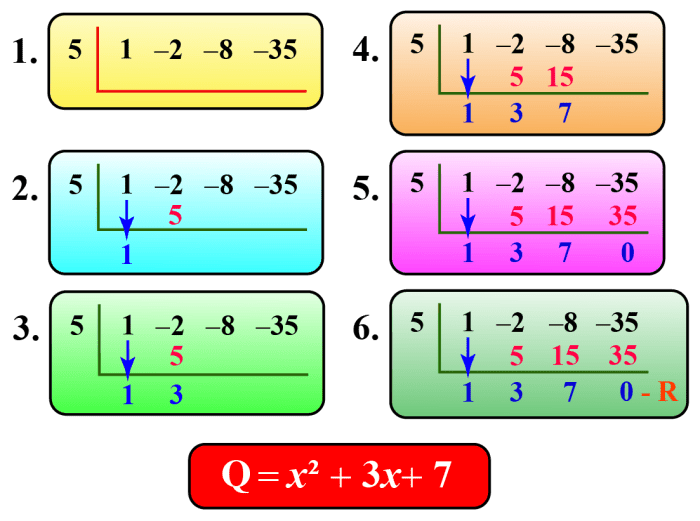
What remainder is represented by the synthetic division below – Embarking on an exploration of what remainder is represented by synthetic division, this comprehensive guide unveils the intricacies of this mathematical technique, providing a lucid explanation of its concept, applications, and implications. Synthetic division, a powerful tool in polynomial division, offers a simplified approach to dividing polynomials, yielding valuable insights into the relationship between the dividend and divisor.
Delving deeper into the significance of the remainder, we discover its pivotal role in determining the validity of division problems and its utility in polynomial division. Moreover, extended synthetic division, an advanced variation of the technique, extends its capabilities, providing a more efficient method for polynomial division.
Synthetic Division Remainder: What Remainder Is Represented By The Synthetic Division Below
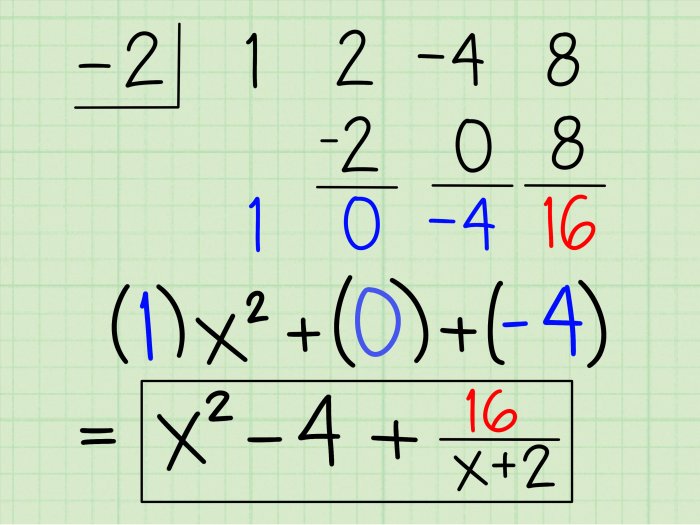
Synthetic division is a mathematical technique used to divide a polynomial by a linear factor (a polynomial of degree 1). It provides a systematic and efficient method to find the quotient and remainder of the division.
Interpreting the Remainder
The remainder in synthetic division is significant because it represents the value of the polynomial at the divisor. If the remainder is zero, it indicates that the dividend is divisible by the divisor. If the remainder is non-zero, it means that the dividend is not divisible by the divisor.
Applications of the Remainder
The remainder in synthetic division has various applications in mathematics, including:
- Checking the validity of a division problem
- Solving polynomial equations
- Finding the roots of a polynomial
Extended Synthetic Division, What remainder is represented by the synthetic division below
Extended synthetic division is a variation of synthetic division that can be used to divide a polynomial by a quadratic factor (a polynomial of degree 2). It follows the same principles as synthetic division, but with additional steps to account for the higher degree of the divisor.
Extended synthetic division is particularly useful when the divisor is a quadratic factor that cannot be factored further. It provides a systematic and efficient way to find the quotient and remainder of the division.
FAQ Corner
What is synthetic division?
Synthetic division is a simplified method of polynomial division that involves arranging the coefficients of the dividend and divisor in a specific pattern, allowing for efficient division.
How do I interpret the remainder in synthetic division?
The remainder in synthetic division represents the value of the dividend when divided by the divisor. A zero remainder indicates that the divisor is a factor of the dividend, while a non-zero remainder signifies that the divisor is not a factor.
What are the applications of synthetic division?
Synthetic division finds applications in polynomial division, checking the validity of division problems, and solving various mathematical problems involving polynomials.