Practice 5-3 Transforming Parabolas Answers provides a thorough examination of the intriguing world of transforming parabolas. This comprehensive guide delves into the fundamental concepts, practical applications, and diverse transformations that shape these mathematical curves.

Throughout this exploration, we will unravel the mysteries of parabolas, from their vertex form to their standard form, while uncovering the real-world applications that make them indispensable tools in various fields.

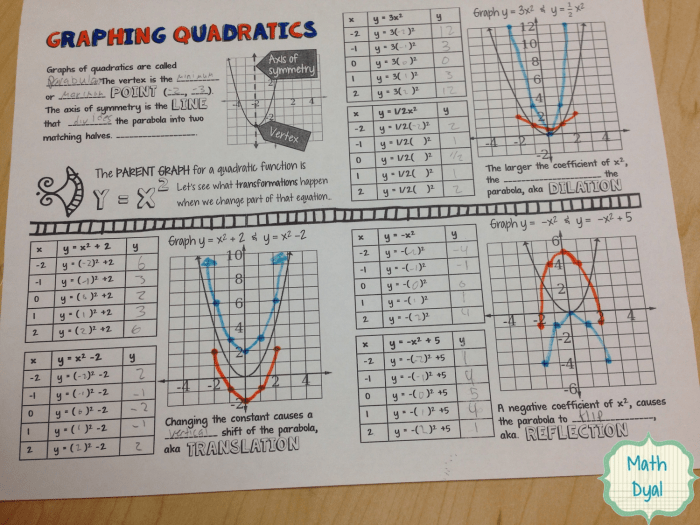
Transforming Parabolas

Transforming parabolas involves manipulating the equation of a parabola to shift, stretch, or shrink the graph without changing its basic shape. This allows for the analysis and application of parabolas in various contexts.

Parabolas can be transformed in several ways, including:

• Translating: Moving the parabola horizontally or vertically.
• Reflecting: Flipping the parabola across the x- or y-axis.
• Stretching or shrinking: Changing the width or height of the parabola.

Vertex Form, Practice 5-3 transforming parabolas answers

The vertex form of a parabola is given by the equation y = a(x- h)^2 + k , where (h, k) is the vertex of the parabola. This form allows for easy identification of the vertex and determination of the parabola’s shape and orientation.

To transform a parabola into vertex form, complete the square or use the transformations mentioned earlier to shift the parabola until its vertex is at the origin.

Standard Form

The standard form of a parabola is given by the equation y = ax^2 + bx + c. This form is useful for finding the x- and y-intercepts of the parabola, as well as for determining its symmetry and concavity.

To transform a parabola into standard form, use the square root property or the transformations discussed previously to manipulate the equation until it is in the desired form.

Applications

Transforming parabolas has numerous real-world applications, including:

• Modeling projectile motion: The trajectory of a projectile can be represented by a parabola.
• Designing parabolic reflectors: The shape of parabolic reflectors is used to focus light or sound waves.
• Analyzing the flight of airplanes: The path of an airplane can be approximated by a parabola.

Expert Answers: Practice 5-3 Transforming Parabolas Answers

What is the significance of the vertex form of a parabola?

The vertex form of a parabola, y = a(x – h)^2 + k, provides valuable insights into the parabola’s key characteristics. It reveals the vertex coordinates (h, k), which represent the parabola’s turning point, and the parameter ‘a’, which determines the parabola’s shape and orientation.

How can I transform a parabola into standard form?

To transform a parabola into standard form, y = ax^2 + bx + c, follow these steps: 1) Complete the square to eliminate the x-term; 2) Factor out the coefficient ‘a’ from the quadratic term; 3) Simplify the equation by rearranging the constants.